打了一天，最后只写出了三道题，菜醒，先把wp写了

Web

没想到web也有被社工压力的一天，打开题目四条朋友圈

第三条中隐藏个URL

http://61.147.171.105:56751/secret/find_my_password

需要找到四个信息

1.邮箱在第四条小说属性详细信息中；

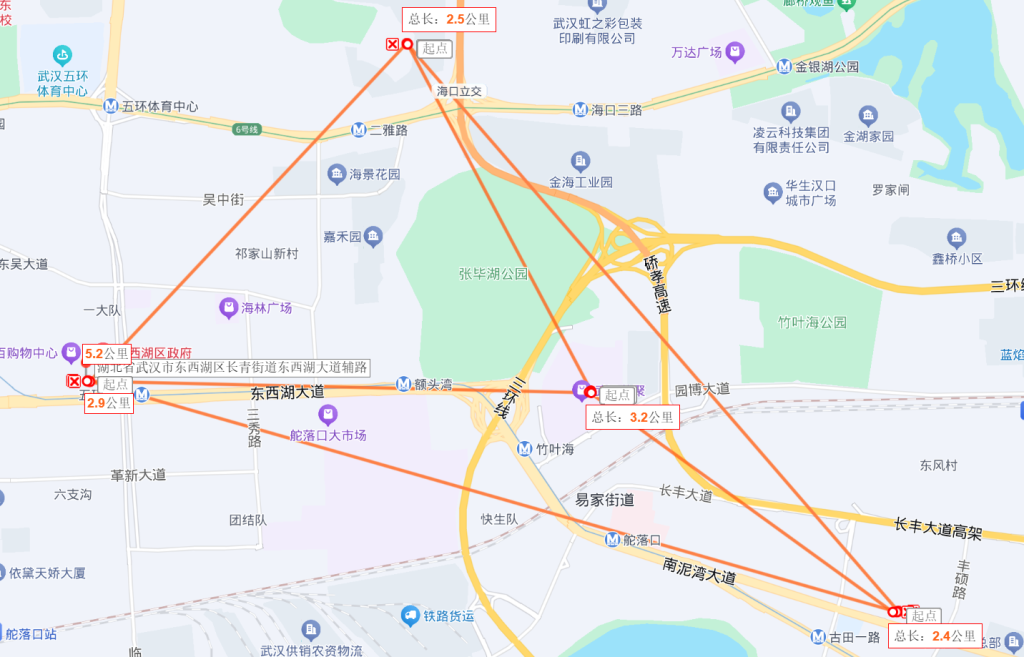
2.经纬度第一条朋友圈可以找到

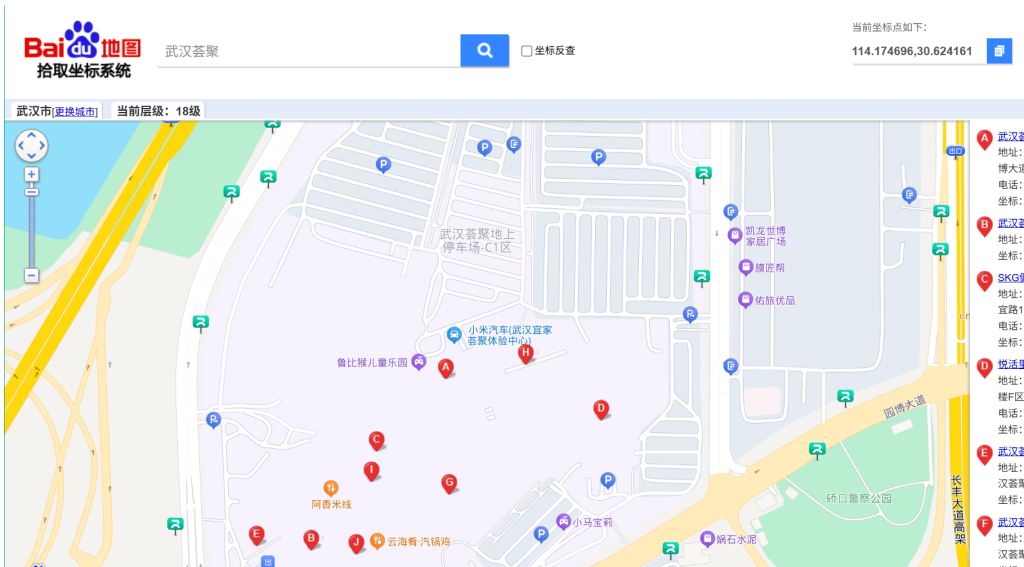
3.老家地址和英文名用航旅纵横扫一扫可出

提交后访问新路由

查看源码目录穿越到/flag

Crypto

EzECDSA

分析附件从以下方面进行攻击

格攻击(Lattice Attack)
1. 将签名方程转化为格结构
2. 使用LLL算法进行格约简
3. 在短向量中寻找私钥候选值
4. 时间复杂度：O(t³)，t为签名数量
改进格攻击(Advanced Lattice Attack)
1. 专门针对二次递归nonce设计
2. 增加格维度以包含递归参数a, b, c
3. 利用二次关系建立扩展方程组
4. 比标准格攻击更高效处理递归关系
Gröbner基攻击
1. 构建包含私钥和递归参数的多项式理想
2. 计算Gröbner基将方程组三角化
3. 直接从基中提取私钥
4. 特别适合处理非线性方程组
多项式求根攻击
1. 通过差分方程消去递归参数
2. 构建仅含私钥的多项式方程
3. 在有限域上求多项式根
4. 最高效的确定性方法（当有效时）
子集攻击
1. 尝试不同的签名子集组合
2. 解决特定签名组合导致数值问题的情况
3. 增加攻击的鲁棒性和成功率

from sage.all import *
import hashlib

# NIST P-256曲线参数
p = 0xFFFFFFFF00000001000000000000000000000000FFFFFFFFFFFFFFFFFFFFFFFF
a_curve = 0xFFFFFFFF00000001000000000000000000000000FFFFFFFFFFFFFFFFFFFFFFFC
b_curve = 0x5AC635D8AA3A93E7B3EBBD55769886BC651D06B0CC53B0F63BCE3C3E27D2604B
n = 0xFFFFFFFF00000000FFFFFFFFFFFFFFFFBCE6FAADA7179E84F3B9CAC2FC632551
F = GF(p)
E = EllipticCurve(F, [a_curve, b_curve])

# 签名数据
signatures = [
    (5832921593739954772384341732387581797486339670895875430934592373351528180781, 
     78576287416983546819312440403592484606132915965726128924031253623117138586396, 
     108582979377193966287732302562639670357586761346333866965382465209612237330851),
    (85517239535736342992982496475440962888226294744294285419613128065975843025446, 
     60425040031360920373082268221766168683222476464343035165195057634060216692194, 
     27924509924269609509672965613674355269361001011362007412205784446375567959036),
    (90905761421138489726836357279787648991884324454425734512085180879013704399530, 
     75779605492148881737630918749717271960050893072832415117470852442721700807111, 
     72740499400319841565890543635298470075267336863033867770902108413176557795256),
    (103266614372002123398101167242562044737358751274736728792365384600377408313142, 
     89519601474973769723244654516140957004170211982048028366151899055366457476708, 
     23639647021855356876198750083669161995553646511611903128486429649329358343588),
    (9903460667647154866199928325987868915846235162578615698288214703794150057571, 
     17829304522948160053211214227664982869100868125268116260967204562276608388692, 
     74400189461172040580877095515356365992183768921088660926738652857846750009205),
    (54539896686295066164943194401294833445622227965487949234393615233511802974126, 
     66428683990399093855578572760918582937085121375887639383221629490465838706027, 
     25418035697368269779911580792368595733749376383350120613502399678197333473802)
]

def validate_private_key(d_candidate, signatures, n):
    """验证恢复的私钥是否正确"""
    try:
        # 验证前三个签名
        for i, (h, r, s) in enumerate(signatures[:3]):
            s_inv = pow(s, -1, n)
            k_candidate = (s_inv * (h + r * d_candidate)) % n
            
            # 重新计算签名验证
            s_verif = (pow(k_candidate, -1, n) * (h + r * d_candidate)) % n
            if s_verif != s:
                return False
        return True
    except:
        return False

def lattice_attack(signatures, n):
    """基本格攻击方法"""
    t = len(signatures)
    B = matrix(ZZ, t+1, t+1)
    
    # 设置格的右下角子矩阵为n*I
    for i in range(t):
        B[i, i] = n
    
    # 设置格的最后一列
    for i in range(t):
        h, r, s = signatures[i]
        s_inv = pow(s, -1, n)
        B[t, i] = int(s_inv * r) % n
    
    # 设置格的最后一列
    B[t, t] = 1
    
    # 设置格的最后一行
    for i in range(t):
        h, r, s = signatures[i]
        s_inv = pow(s, -1, n)
        B[i, t] = int(s_inv * h) % n
    
    # 使用LLL算法进行格约简
    B_lll = B.LLL()
    
    # 寻找包含私钥的短向量
    for row in B_lll:
        if row[t] == 0:  # 跳过零向量
            continue
        if abs(row[t]) == 1:  # 找到候选私钥
            d_candidate = -row[0] * pow(row[t], -1, n) % n
            if validate_private_key(d_candidate, signatures, n):
                return d_candidate
    
    return None

def advanced_lattice_attack(signatures, n):
    """针对二次递归nonce的改进格攻击"""
    t = len(signatures)
    m = 4  # 未知参数数量 (a, b, c, d)
    
    # 创建格
    lattice = matrix(ZZ, t + m, t + m)
    
    # 设置单位矩阵部分
    for i in range(t):
        lattice[i, i] = 1
    
    # 设置右下角为n*I
    for i in range(t, t + m):
        lattice[i, i] = n
    
    # 填充方程系数
    for i in range(t - 2):
        h0, r0, s0 = signatures[i]
        h1, r1, s1 = signatures[i+1]
        h2, r2, s2 = signatures[i+2]
        
        # 系数计算
        s0_inv = pow(s0, -1, n)
        s1_inv = pow(s1, -1, n)
        k0_term = (s0_inv * r0) % n
        k1_term = (s1_inv * r1) % n
        
        # 二次关系系数
        lattice[i, t] = (k0_term**2) % n
        lattice[i, t+1] = k0_term % n
        lattice[i, t+2] = 1
        lattice[i, t+3] = (s0_inv * h0 - s1_inv * h1) % n
    
    # LLL格约简
    reduced_lattice = lattice.LLL()
    
    # 寻找短向量
    for row in reduced_lattice:
        if row[-1] == 0:  # 跳过最后元素为零的行
            continue
        d_candidate = abs(row[-1])
        if validate_private_key(d_candidate, signatures, n):
            return d_candidate
    
    return None

def groebner_attack(signatures, n):
    """Gröbner基攻击方法"""
    P.<d, a, b, c> = PolynomialRing(Zmod(n), order='lex')
    
    equations = []
    k_values = []
    
    # 创建k_i的多项式
    for i, (h, r, s) in enumerate(signatures):
        s_inv = pow(s, -1, n)
        k = s_inv * (h + d * r)
        k_values.append(k)
    
    # 添加递归关系方程
    for i in range(len(signatures) - 1):
        # k_{i+1} = a*k_i^2 + b*k_i + c
        eq = k_values[i+1] - (a * k_values[i]^2 + b * k_values[i] + c)
        equations.append(eq)
    
    # 创建理想并计算Gröbner基
    I = P.ideal(equations)
    G = I.groebner_basis()
    
    # 求解私钥d
    if G:
        for poly in G:
            if poly.degree() == 1 and poly.lm() == d:
                d_candidate = -poly.constant_coefficient() % n
                if validate_private_key(d_candidate, signatures, n):
                    return d_candidate
    
    return None

def polynomial_attack(signatures, n):
    """多项式求根攻击"""
    R.<d> = PolynomialRing(Zmod(n), 'd')
    
    # 使用4个连续签名构建方程组
    k_polys = []
    for i in range(4):
        h, r, s = signatures[i]
        s_inv = pow(s, -1, n)
        k_poly = s_inv * (h + d * r)
        k_polys.append(k_poly)
    
    # 构建差分方程消去参数
    A = k_polys[1] - k_polys[0]
    B = k_polys[2] - k_polys[1]
    C = k_polys[3] - k_polys[2]
    
    # 构造多项式方程 (B^2 - C*A)(k1 - k3) - (C^2 - B*D)(k0 - k2) = 0
    k0, k1, k2, k3 = k_polys
    eq = (B^2 - C*A) * (k1 - k3) - (C^2 - B*(k_polys[3]-k_polys[2])) * (k0 - k2)
    
    # 求根
    roots = eq.roots()
    for root, mult in roots:
        d_candidate = int(root)
        if validate_private_key(d_candidate, signatures, n):
            return d_candidate
    
    return None

def recover_flag(private_key):
    """从私钥恢复flag"""
    # 原始消息用于验证
    messages = [
        b"Hello player, welcome to L3HCTF 2025!",
        b"This is a crypto challenge, as you can probably tell.",
        b"It's about ECDSA, a very... robust algorithm.",
        b"I'm sure there are no implementation flaws whatsoever.",
        b"Anyway, here are your signatures. Good luck!",
        f"Oh, and the flag is L3HCTF{{{private_key}}}. Don't tell anyone!".encode(),
    ]
    
    # 验证最后一条消息
    h_flag = int.from_bytes(hashlib.sha256(messages[5]).digest(), 'big')
    h_sig = signatures[5][0]
    
    if h_flag == h_sig:
        return f"L3HCTF{{{private_key}}}"
    return None

def main_attack():
    """主攻击函数，尝试多种方法恢复私钥"""
    print("=== 尝试基本格攻击 ===")
    d_candidate = lattice_attack(signatures, n)
    if d_candidate:
        print(f"成功恢复私钥: {d_candidate}")
        flag = recover_flag(d_candidate)
        if flag:
            return flag
    
    print("\n=== 尝试改进格攻击（针对二次递归）===")
    d_candidate = advanced_lattice_attack(signatures, n)
    if d_candidate:
        print(f"成功恢复私钥: {d_candidate}")
        flag = recover_flag(d_candidate)
        if flag:
            return flag
    
    print("\n=== 尝试Gröbner基攻击 ===")
    d_candidate = groebner_attack(signatures, n)
    if d_candidate:
        print(f"成功恢复私钥: {d_candidate}")
        flag = recover_flag(d_candidate)
        if flag:
            return flag
    
    print("\n=== 尝试多项式求根攻击 ===")
    d_candidate = polynomial_attack(signatures, n)
    if d_candidate:
        print(f"成功恢复私钥: {d_candidate}")
        flag = recover_flag(d_candidate)
        if flag:
            return flag
    
    print("\n=== 尝试子集攻击 ===")
    # 尝试不同的签名子集组合
    for subset_size in range(4, 7):
        for i in range(len(signatures) - subset_size + 1):
            subset = signatures[i:i+subset_size]
            print(f"尝试子集 {i}到{i+subset_size-1} (大小={subset_size})")
            
            # 尝试所有攻击方法在子集上
            d_candidate = lattice_attack(subset, n)
            if not d_candidate:
                d_candidate = advanced_lattice_attack(subset, n)
            if not d_candidate:
                d_candidate = groebner_attack(subset, n)
            if not d_candidate:
                d_candidate = polynomial_attack(subset, n)
            
            if d_candidate and validate_private_key(d_candidate, signatures, n):
                print(f"成功恢复私钥: {d_candidate}")
                flag = recover_flag(d_candidate)
                if flag:
                    return flag
    
    return None

if __name__ == "__main__":
    flag = main_attack()
    
    if flag:
        print("\n" + "="*50)
        print(f"成功恢复FLAG: {flag}")
        print("="*50)
    else:
        print("\n未能恢复私钥，请尝试其他方法或检查输入数据")

math_problem

先解密出p和q

# SageMath 代码
p_bits = 512
known_bits = 400
unknown_bits = p_bits - known_bits

# 从 Python 输出加载值
m_val = 89976238182539956361646502174582239233867602786630733592087980565136028257351416845669763032829951111889837196225697003100579641554184101899334531827940735063578835944600821891388396352487725296846958330005131539072371256697512444779913966988812704198431594797297087795356209894849648037186106182879820249927
e_val = 1485680028344144006765555653772516703832059493333760848397113959350969611961772611966978839643079277183666542572626814999

# 创建模 m_val 的多项式环
P.<x> = PolynomialRing(Zmod(m_val))

# 计算 2^400 在模 m_val 下的逆元
inv_2_400 = inverse_mod(2^known_bits, m_val)

# 构造首一多项式：g(x) = x + e_val * inv_2_400
t = e_val * inv_2_400
g = x + t

# 设置 x 的边界
X = 2^unknown_bits  # 2^112

# 使用 Coppersmith 方法
roots = g.small_roots(X=X, beta=0.5)

if roots:
    x0 = roots[0]
    # 从根恢复 p
    p_candidate = int(2^known_bits * x0 + e_val)
    
    # 验证 p_candidate 是否整除 m_val
    if m_val % p_candidate == 0:
        p = p_candidate
        q = m_val // p_candidate
        print(f'p = {p}')
        print(f'q = {q}')
        
        # 验证
        if p * q == m_val:
            print("验证成功: p * q == m_val")
        else:
            print("验证失败")
    else:
        print("错误: p_candidate 不能整除 m_val")
else:
    print("错误: 未找到根")

解密flag部分：

from Crypto.Util.number import long_to_bytes
import gmpy2

# 给定数据
n = 1031361339208727791691298627543660626410606240120564103678654539403400080866317968868129842196968695881908504164493307869679126969820723174066217814377008485456923379924853652121682069359767219423414060835725846413022799109637665041081215491777412523849107017649039242068964400703052356256244423474207673552341406331476528847104738461329766566162770505123490007005634713729116037657261941371410447717090137275138353217951485412890440960756321099770208574858093921
c = 102236458296005878146044806702966879940747405722298512433320216536239393890381990624291341014929382445849345903174490221598574856359809965659167404530660264493014761156245994411400111564065685663103513911577275735398329066710295262831185375333970116921093419001584290401132157702732101670324984662104398372071827999099732380917953008348751083912048254277463410132465011554297806390512318512896160903564287060978724650580695287391837481366347198300815022619675984
r = 11462596792681484119885867626229848343628572981903327079472959385609791492187597506621130701780561699379556165436984737148828369344212127061312661920652823

# 从 SageMath 输出获取的 p 和 q
p = 10131840248837038199009829519775750424799329778826965567641085303764923942459699675684256950985404319256009819736357506324552460305994284453952660375382039
q = 8880542524628503503088519580251341265303330988486163026964989899094554424819704451400137548766462436771110504734327527344318689549280294343934878659187793

# 验证 n = p * q * r
n_recovered = p * q * r
if n_recovered != n:
    raise ValueError(f"恢复的 n 不匹配: {n_recovered} != {n}")
print("[+] n 验证成功")

# 计算 φ(n) = (p-1)(q-1)(r-1)
phi = (p-1) * (q-1) * (r-1)

# 计算私钥
e = 65537
d = gmpy2.invert(e, phi)

# 解密密文
m = pow(c, d, n)
flag = long_to_bytes(m)

print(f"\n[+] 解密成功! Flag: {flag.decode()}")

Web

Crypto

EzECDSA

math_problem

发送评论 编辑评论

推荐文章

发送评论编辑评论